12. Optimal Taxation in an LQ Economy#
In addition to what’s in Anaconda, this lecture will need the following libraries:
!pip install --upgrade quantecon
12.1. Overview#
In this lecture, we study optimal fiscal policy in a linear quadratic setting.
We modify a model of Robert Lucas and Nancy Stokey [Lucas and Stokey, 1983] so that convenient formulas for solving linear-quadratic models can be applied.
The economy consists of a representative household and a benevolent government.
The government finances an exogenous stream of government purchases with state-contingent loans and a linear tax on labor income.
A linear tax is sometimes called a flat-rate tax.
The household maximizes utility by choosing paths for consumption and labor, taking prices and the government’s tax rate and borrowing plans as given.
Maximum attainable utility for the household depends on the government’s tax and borrowing plans.
The Ramsey problem [Ramsey, 1927] is to choose tax and borrowing plans that maximize the household’s welfare, taking the household’s optimizing behavior as given.
There is a large number of competitive equilibria indexed by different government fiscal policies.
The Ramsey planner chooses the best competitive equilibrium.
We want to study the dynamics of tax rates, tax revenues, government debt under a Ramsey plan.
Because the Lucas and Stokey model features state-contingent government debt, the government debt dynamics differ substantially from those in a model of Robert Barro [Barro, 1979].
The treatment given here closely follows this manuscript, prepared by Thomas J. Sargent and Francois R. Velde.
We cover only the key features of the problem in this lecture, leaving you to refer to that source for additional results and intuition.
We’ll need the following imports:
import sys
import numpy as np
import matplotlib.pyplot as plt
from numpy import sqrt, eye, zeros, cumsum
from numpy.random import randn
import scipy.linalg
from collections import namedtuple
from quantecon import nullspace, mc_sample_path, var_quadratic_sum
12.1.1. Model Features#
Linear quadratic (LQ) model
Representative household
Stochastic dynamic programming over an infinite horizon
Distortionary taxation
12.2. The Ramsey Problem#
We begin by outlining the key assumptions regarding technology, households and the government sector.
12.2.1. Technology#
Labor can be converted one-for-one into a single, non-storable consumption good.
In the usual spirit of the LQ model, the amount of labor supplied in each period is unrestricted.
This is unrealistic, but helpful when it comes to solving the model.
Realistic labor supply can be induced by suitable parameter values.
12.2.2. Households#
Consider a representative household who chooses a path
subject to the budget constraint
Here
The scaled Arrow-Debreu price
If we let
Thus, our scaled Arrow-Debreu price is the ordinary Arrow-Debreu price multiplied by the discount factor
The budget constraint (12.2) requires that the present value of consumption be restricted to equal the present value of endowments, labor income and coupon payments on bond holdings.
12.2.3. Government#
The government imposes a linear tax on labor income, fully committing to a stochastic path of tax rates at time zero.
The government also issues state-contingent debt.
Given government tax and borrowing plans, we can construct a competitive equilibrium with distorting government taxes.
Among all such competitive equilibria, the Ramsey plan is the one that maximizes the welfare of the representative consumer.
12.2.4. Exogenous Variables#
Endowments, government expenditure, the preference shock process
The matrices
We consider two specifications for
Discrete case:
VAR case:
12.2.5. Feasibility#
The period-by-period feasibility restriction for this economy is
A labor-consumption process
12.2.6. Government Budget Constraint#
Where
12.2.7. Equilibrium#
An equilibrium is a feasible allocation
The allocation
The government’s budget constraint (12.4) is satisfied.
The Ramsey problem is to choose the equilibrium
If
The solution procedure we adopt is
Use the first-order conditions from the household problem to pin down prices and allocations given
Use these expressions to rewrite the government budget constraint (12.4) in terms of exogenous variables and allocations.
Maximize the household’s objective function (12.1) subject to the constraint constructed in step 2 and the feasibility constraint (12.3).
The solution to this maximization problem pins down all quantities of interest.
12.2.8. Solution#
Step one is to obtain the first-conditions for the household’s problem, taking taxes and prices as given.
Letting
Rearranging and normalizing at
Substituting (12.5) into the government’s budget constraint (12.4) yields
The Ramsey problem now amounts to maximizing (12.1) subject to (12.6) and (12.3).
The associated Lagrangian is
The first-order conditions associated with
and
Combining these last two equalities with (12.3) and working through the algebra, one can show that
where
Apart from
To solve for
The term inside the brackets in (12.6) is
Using (12.8), the definitions above and the fact that
Reinserting into (12.6), we get
Although it might not be clear yet, we are nearly there because:
The two expectations terms in (12.9) can be solved for in terms of model primitives.
This in turn allows us to solve for the Lagrange multiplier
With
Once we have the allocations, prices and the tax system can be derived from (12.5).
12.2.9. Computing the Quadratic Term#
Let’s consider how to obtain the term
If we can compute the two expected geometric sums
then the problem reduces to solving
for
Provided that
Let’s work out how to compute mathematical expectations in (12.10).
For the first one, the random variable
For the second expectation in (12.10), the random variable
It follows that both objects of interest are special cases of the expression
where
Suppose first that
In this case, the formula for computing
The first equation is known as a discrete Lyapunov equation and can be solved using this function.
12.2.10. Finite State Markov Case#
Next, suppose that
Suppose further that each
Let
For example, in the discussion above,
It is legitimate to pass the expectation through the sum, leading to
Here
It can be shown that (12.12) is in fact equal to the
This last fact is applied in the calculations below.
12.2.11. Other Variables#
We are interested in tracking several other variables besides the ones described above.
To prepare the way for this, we define
as the scaled Arrow-Debreu time
These are prices that would prevail at time
These prices are constituents of the present value of government obligations outstanding at time
Using our expression for prices and the Ramsey plan, we can also write
This version is more convenient for computation.
Using the equation
it is possible to verify that (12.13) implies that
and
Define
12.2.12. A Martingale#
We now want to study the following two objects, namely,
and the cumulation of
The term
Thus,
Use expressions (12.14) and (12.15) to obtain
or
where
It follows from equation (12.16) that
which asserts that
In the tax-smoothing model of Robert Barro [Barro, 1979], government debt is a random walk.
In the current model, government debt excess payoff
12.3. Implementation#
The following code provides functions for
Solving for the Ramsey plan given a specification of the economy.
Simulating the dynamics of the major variables.
Description and clarifications are given below
# Set up a namedtuple to store data on the model economy
Economy = namedtuple('economy',
('β', # Discount factor
'Sg', # Govt spending selector matrix
'Sd', # Exogenous endowment selector matrix
'Sb', # Utility parameter selector matrix
'Ss', # Coupon payments selector matrix
'discrete', # Discrete or continuous -- boolean
'proc')) # Stochastic process parameters
# Set up a namedtuple to store return values for compute_paths()
Path = namedtuple('path',
('g', # Govt spending
'd', # Endowment
'b', # Utility shift parameter
's', # Coupon payment on existing debt
'c', # Consumption
'l', # Labor
'p', # Price
'τ', # Tax rate
'rvn', # Revenue
'B', # Govt debt
'R', # Risk-free gross return
'π', # One-period risk-free interest rate
'Π', # Cumulative rate of return, adjusted
'ξ')) # Adjustment factor for Π
def compute_paths(T, econ):
"""
Compute simulated time paths for exogenous and endogenous variables.
Parameters
===========
T: int
Length of the simulation
econ: a namedtuple of type 'Economy', containing
β - Discount factor
Sg - Govt spending selector matrix
Sd - Exogenous endowment selector matrix
Sb - Utility parameter selector matrix
Ss - Coupon payments selector matrix
discrete - Discrete exogenous process (True or False)
proc - Stochastic process parameters
Returns
========
path: a namedtuple of type 'Path', containing
g - Govt spending
d - Endowment
b - Utility shift parameter
s - Coupon payment on existing debt
c - Consumption
l - Labor
p - Price
τ - Tax rate
rvn - Revenue
B - Govt debt
R - Risk-free gross return
π - One-period risk-free interest rate
Π - Cumulative rate of return, adjusted
ξ - Adjustment factor for Π
The corresponding values are flat numpy ndarrays.
"""
# Simplify names
β, Sg, Sd, Sb, Ss = econ.β, econ.Sg, econ.Sd, econ.Sb, econ.Ss
if econ.discrete:
P, x_vals = econ.proc
else:
A, C = econ.proc
# Simulate the exogenous process x
if econ.discrete:
state = mc_sample_path(P, init=0, sample_size=T)
x = x_vals[:, state]
else:
# Generate an initial condition x0 satisfying x0 = A x0
nx, nx = A.shape
x0 = nullspace((eye(nx) - A))
x0 = -x0 if (x0[nx-1] < 0) else x0
x0 = x0 / x0[nx-1]
# Generate a time series x of length T starting from x0
nx, nw = C.shape
x = zeros((nx, T))
w = randn(nw, T)
x[:, 0] = x0.T
for t in range(1, T):
x[:, t] = A @ x[:, t-1] + C @ w[:, t]
# Compute exogenous variable sequences
g, d, b, s = ((S @ x).flatten() for S in (Sg, Sd, Sb, Ss))
# Solve for Lagrange multiplier in the govt budget constraint
# In fact we solve for ν = lambda / (1 + 2*lambda). Here ν is the
# solution to a quadratic equation a(ν**2 - ν) + b = 0 where
# a and b are expected discounted sums of quadratic forms of the state.
Sm = Sb - Sd - Ss
# Compute a and b
if econ.discrete:
ns = P.shape[0]
F = scipy.linalg.inv(eye(ns) - β * P)
a0 = 0.5 * (F @ (x_vals.T @ Sm.T)**2)[0]
H = ((Sb - Sd + Sg) @ x_vals) * ((Sg - Ss) @ x_vals)
b0 = 0.5 * (F @ H.T)[0]
a0, b0 = float(a0[0]), float(b0[0])
else:
H = Sm.T @ Sm
a0 = 0.5 * var_quadratic_sum(A, C, H, β, x0)
H = (Sb - Sd + Sg).T @ (Sg + Ss)
b0 = 0.5 * var_quadratic_sum(A, C, H, β, x0)
# Test that ν has a real solution before assigning
warning_msg = """
Hint: you probably set government spending too {}. Elect a {}
Congress and start over.
"""
disc = a0**2 - 4 * a0 * b0
if disc >= 0:
ν = 0.5 * (a0 - sqrt(disc)) / a0
else:
print("There is no Ramsey equilibrium for these parameters.")
print(warning_msg.format('high', 'Republican'))
sys.exit(0)
# Test that the Lagrange multiplier has the right sign
if ν * (0.5 - ν) < 0:
print("Negative multiplier on the government budget constraint.")
print(warning_msg.format('low', 'Democratic'))
sys.exit(0)
# Solve for the allocation given ν and x
Sc = 0.5 * (Sb + Sd - Sg - ν * Sm)
Sl = 0.5 * (Sb - Sd + Sg - ν * Sm)
c = (Sc @ x).flatten()
l = (Sl @ x).flatten()
p = ((Sb - Sc) @ x).flatten() # Price without normalization
τ = 1 - l / (b - c)
rvn = l * τ
# Compute remaining variables
if econ.discrete:
H = ((Sb - Sc) @ x_vals) * ((Sl - Sg) @ x_vals) - (Sl @ x_vals)**2
temp = (F @ H.T).flatten()
B = temp[state] / p
H = (P[state, :] @ x_vals.T @ (Sb - Sc).T).flatten()
R = p / (β * H)
temp = ((P[state, :] @ x_vals.T @ (Sb - Sc).T)).flatten()
ξ = p[1:] / temp[:T-1]
else:
H = Sl.T @ Sl - (Sb - Sc).T @ (Sl - Sg)
L = np.empty(T)
for t in range(T):
L[t] = var_quadratic_sum(A, C, H, β, x[:, t])
B = L / p
Rinv = (β * ((Sb - Sc) @ A @ x)).flatten() / p
R = 1 / Rinv
AF1 = (Sb - Sc) @ x[:, 1:]
AF2 = (Sb - Sc) @ A @ x[:, :T-1]
ξ = AF1 / AF2
ξ = ξ.flatten()
π = B[1:] - R[:T-1] * B[:T-1] - rvn[:T-1] + g[:T-1]
Π = cumsum(π * ξ)
# Prepare return values
path = Path(g=g, d=d, b=b, s=s, c=c, l=l, p=p,
τ=τ, rvn=rvn, B=B, R=R, π=π, Π=Π, ξ=ξ)
return path
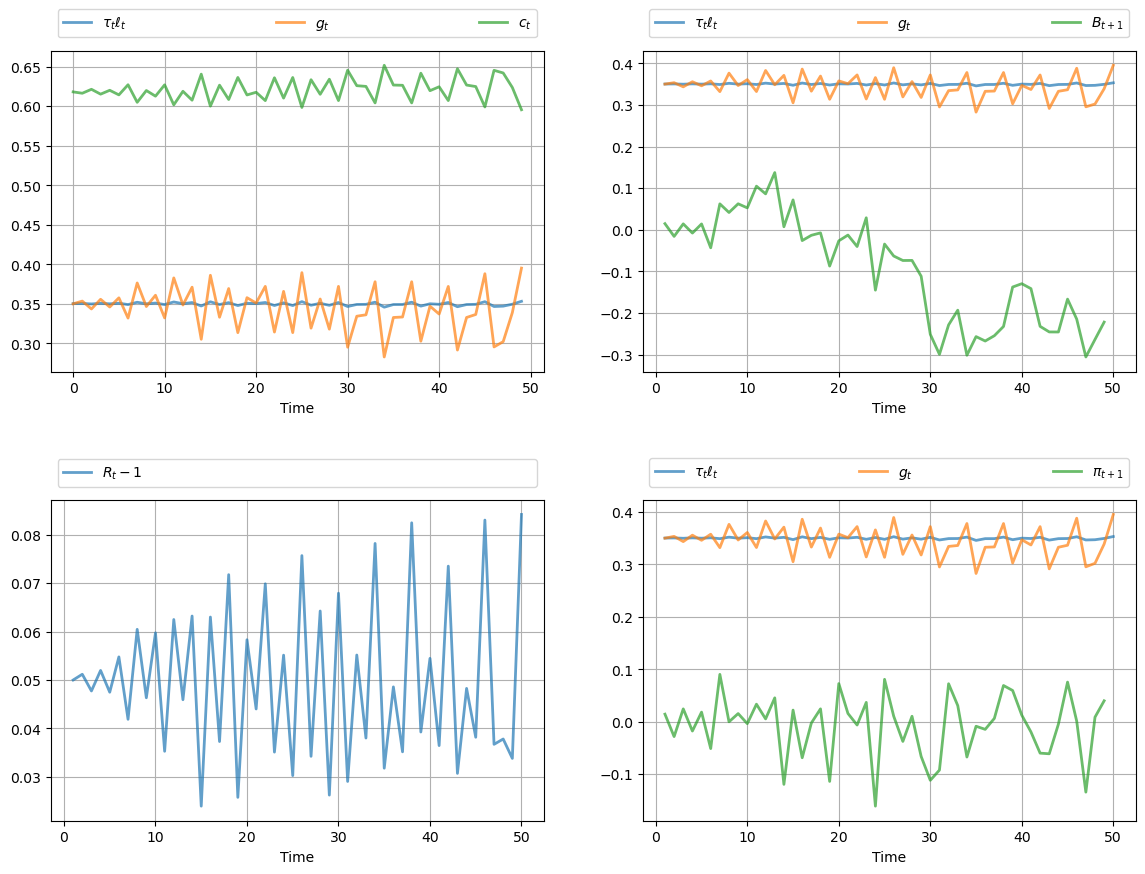
def gen_fig_1(path):
"""
The parameter is the path namedtuple returned by compute_paths(). See
the docstring of that function for details.
"""
T = len(path.c)
# Prepare axes
num_rows, num_cols = 2, 2
fig, axes = plt.subplots(num_rows, num_cols, figsize=(14, 10))
plt.subplots_adjust(hspace=0.4)
for i in range(num_rows):
for j in range(num_cols):
axes[i, j].grid()
axes[i, j].set_xlabel('Time')
bbox = (0., 1.02, 1., .102)
legend_args = {'bbox_to_anchor': bbox, 'loc': 3, 'mode': 'expand'}
p_args = {'lw': 2, 'alpha': 0.7}
# Plot consumption, govt expenditure and revenue
ax = axes[0, 0]
ax.plot(path.rvn, label=r'$\tau_t \ell_t$', **p_args)
ax.plot(path.g, label='$g_t$', **p_args)
ax.plot(path.c, label='$c_t$', **p_args)
ax.legend(ncol=3, **legend_args)
# Plot govt expenditure and debt
ax = axes[0, 1]
ax.plot(list(range(1, T+1)), path.rvn, label=r'$\tau_t \ell_t$', **p_args)
ax.plot(list(range(1, T+1)), path.g, label='$g_t$', **p_args)
ax.plot(list(range(1, T)), path.B[1:T], label='$B_{t+1}$', **p_args)
ax.legend(ncol=3, **legend_args)
# Plot risk-free return
ax = axes[1, 0]
ax.plot(list(range(1, T+1)), path.R - 1, label='$R_t - 1$', **p_args)
ax.legend(ncol=1, **legend_args)
# Plot revenue, expenditure and risk free rate
ax = axes[1, 1]
ax.plot(list(range(1, T+1)), path.rvn, label=r'$\tau_t \ell_t$', **p_args)
ax.plot(list(range(1, T+1)), path.g, label='$g_t$', **p_args)
axes[1, 1].plot(list(range(1, T)), path.π, label=r'$\pi_{t+1}$', **p_args)
ax.legend(ncol=3, **legend_args)
plt.show()
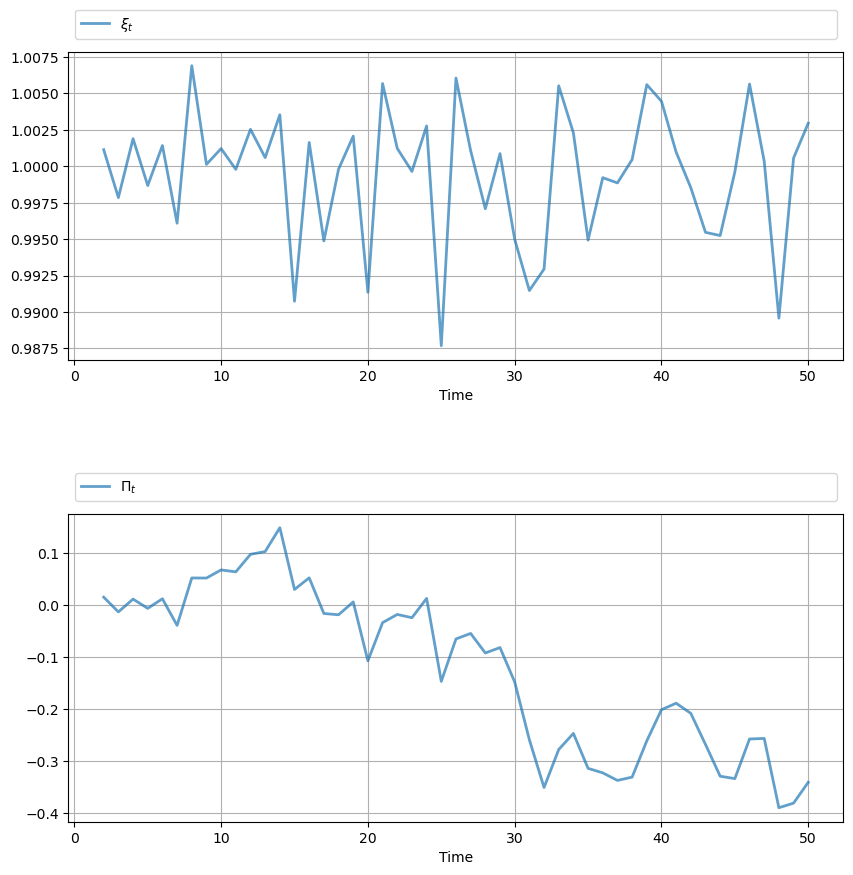
def gen_fig_2(path):
"""
The parameter is the path namedtuple returned by compute_paths(). See
the docstring of that function for details.
"""
T = len(path.c)
# Prepare axes
num_rows, num_cols = 2, 1
fig, axes = plt.subplots(num_rows, num_cols, figsize=(10, 10))
plt.subplots_adjust(hspace=0.5)
bbox = (0., 1.02, 1., .102)
bbox = (0., 1.02, 1., .102)
legend_args = {'bbox_to_anchor': bbox, 'loc': 3, 'mode': 'expand'}
p_args = {'lw': 2, 'alpha': 0.7}
# Plot adjustment factor
ax = axes[0]
ax.plot(list(range(2, T+1)), path.ξ, label=r'$\xi_t$', **p_args)
ax.grid()
ax.set_xlabel('Time')
ax.legend(ncol=1, **legend_args)
# Plot adjusted cumulative return
ax = axes[1]
ax.plot(list(range(2, T+1)), path.Π, label=r'$\Pi_t$', **p_args)
ax.grid()
ax.set_xlabel('Time')
ax.legend(ncol=1, **legend_args)
plt.show()
12.4. Examples#
Let’s look at two examples of usage.
12.4.1. The Continuous Case#
Our first example adopts the VAR specification described above.
Regarding the primitives, we set
Government spending evolves according to
with
Here’s the code
# == Parameters == #
β = 1 / 1.05
ρ, mg = .7, .35
A = eye(2)
A[0, :] = ρ, mg * (1-ρ)
C = np.zeros((2, 1))
C[0, 0] = np.sqrt(1 - ρ**2) * mg / 10
Sg = np.array((1, 0)).reshape(1, 2)
Sd = np.array((0, 0)).reshape(1, 2)
Sb = np.array((0, 2.135)).reshape(1, 2)
Ss = np.array((0, 0)).reshape(1, 2)
economy = Economy(β=β, Sg=Sg, Sd=Sd, Sb=Sb, Ss=Ss,
discrete=False, proc=(A, C))
T = 50
path = compute_paths(T, economy)
gen_fig_1(path)
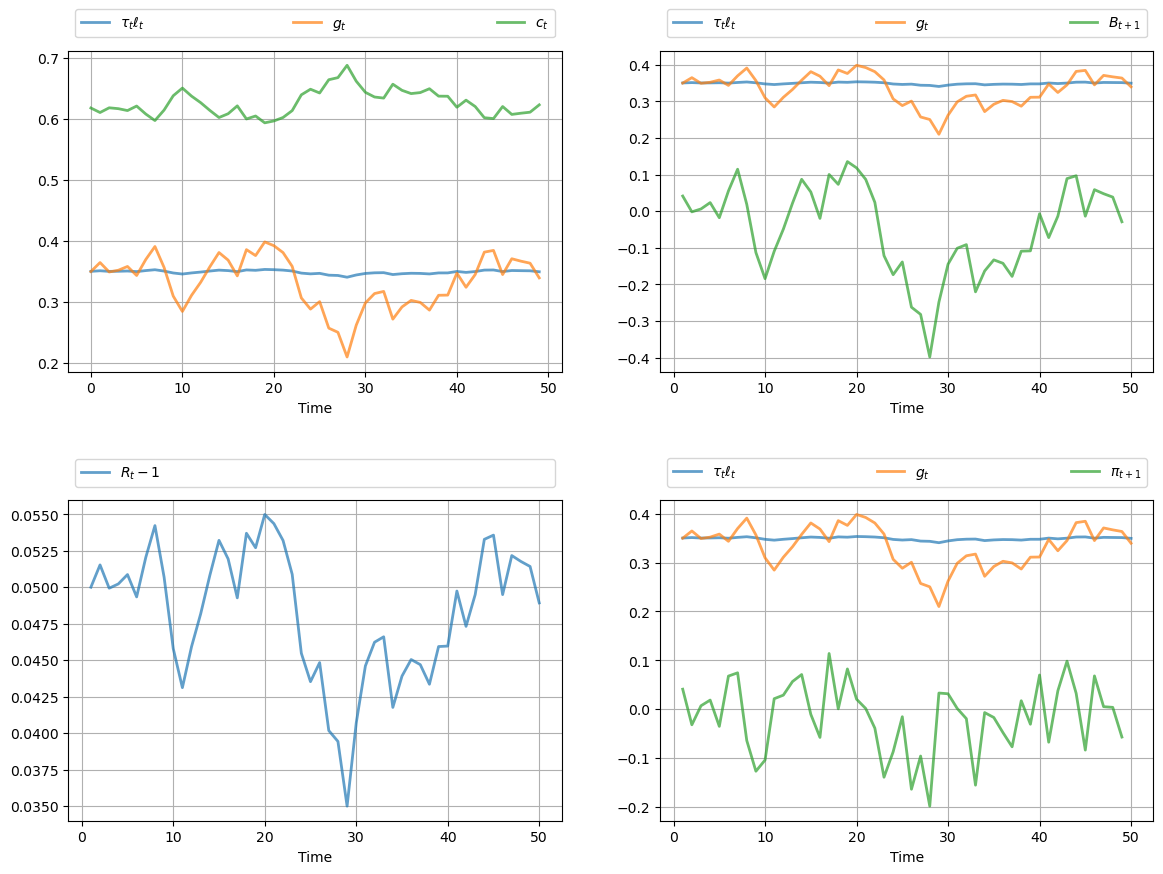
The legends on the figures indicate the variables being tracked.
Most obvious from the figure is tax smoothing in the sense that tax revenue is much less variable than government expenditure.
gen_fig_2(path)
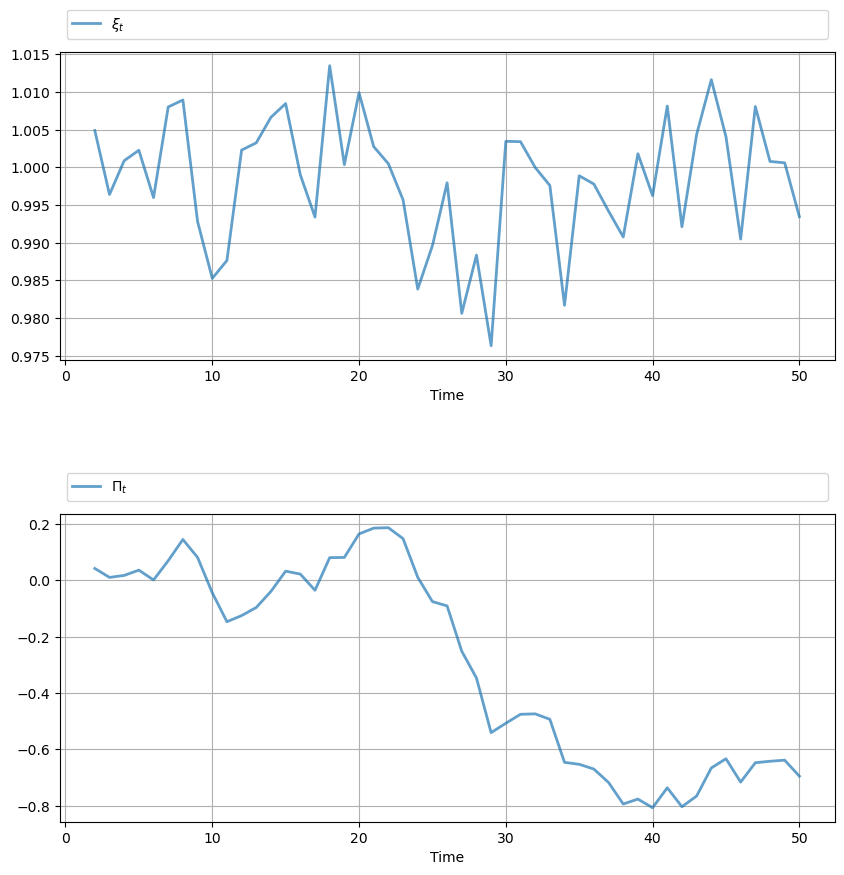
See the original manuscript for comments and interpretation.
12.4.2. The Discrete Case#
Our second example adopts a discrete Markov specification for the exogenous process
# == Parameters == #
β = 1 / 1.05
P = np.array([[0.8, 0.2, 0.0],
[0.0, 0.5, 0.5],
[0.0, 0.0, 1.0]])
# Possible states of the world
# Each column is a state of the world. The rows are [g d b s 1]
x_vals = np.array([[0.5, 0.5, 0.25],
[0.0, 0.0, 0.0],
[2.2, 2.2, 2.2],
[0.0, 0.0, 0.0],
[1.0, 1.0, 1.0]])
Sg = np.array((1, 0, 0, 0, 0)).reshape(1, 5)
Sd = np.array((0, 1, 0, 0, 0)).reshape(1, 5)
Sb = np.array((0, 0, 1, 0, 0)).reshape(1, 5)
Ss = np.array((0, 0, 0, 1, 0)).reshape(1, 5)
economy = Economy(β=β, Sg=Sg, Sd=Sd, Sb=Sb, Ss=Ss,
discrete=True, proc=(P, x_vals))
T = 15
path = compute_paths(T, economy)
gen_fig_1(path)
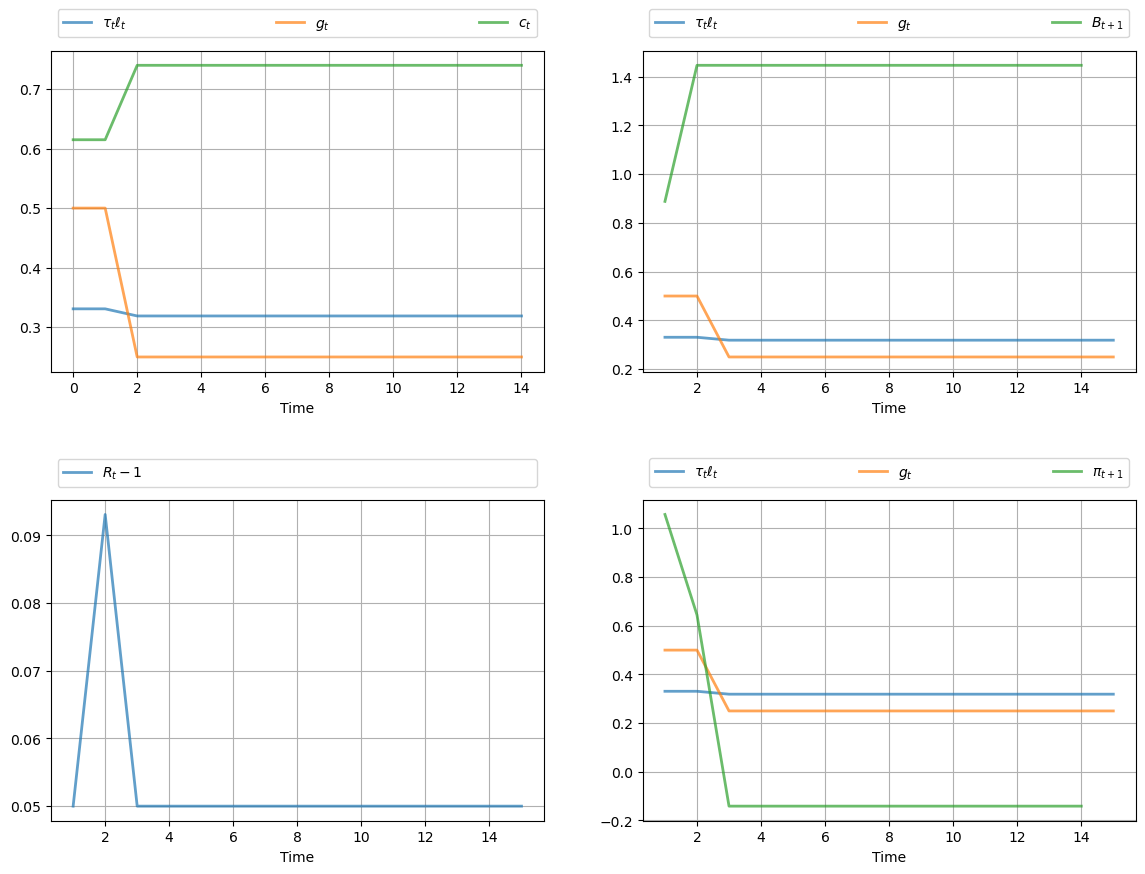
The call gen_fig_2(path) generates
gen_fig_2(path)
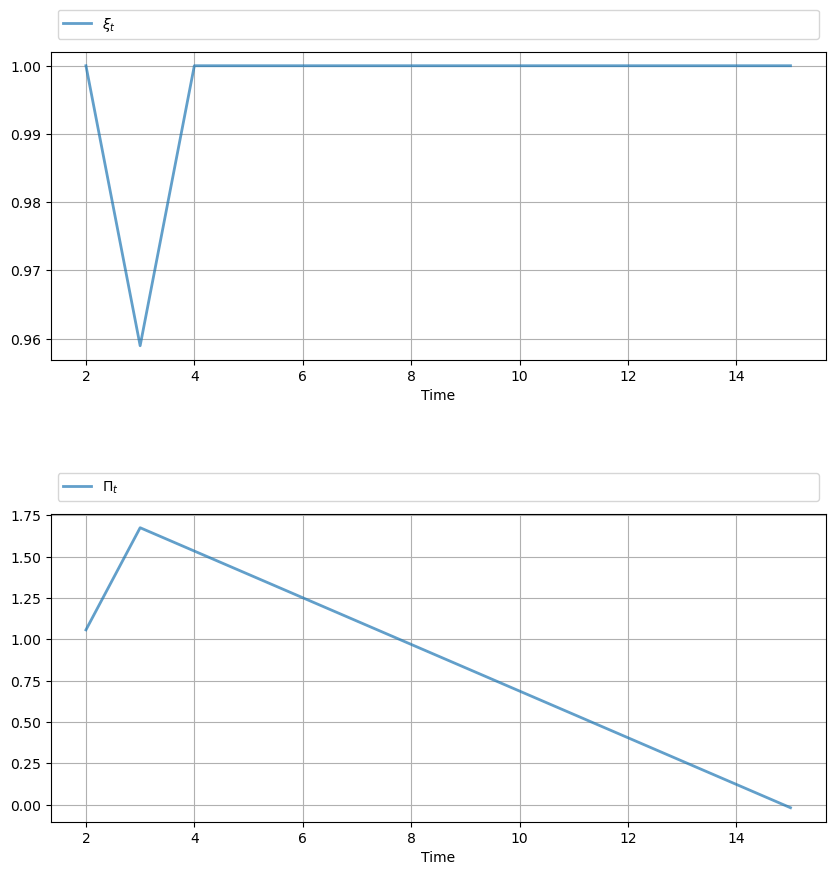
See the original manuscript for comments and interpretation.
12.5. Exercises#
Exercise 12.1
Modify the VAR example given above, setting
with
Produce the corresponding figures.
Solution to Exercise 12.1
# == Parameters == #
β = 1 / 1.05
ρ, mg = .95, .35
A = np.array([[0, 0, 0, ρ, mg*(1-ρ)],
[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 1]])
C = np.zeros((5, 1))
C[0, 0] = np.sqrt(1 - ρ**2) * mg / 8
Sg = np.array((1, 0, 0, 0, 0)).reshape(1, 5)
Sd = np.array((0, 0, 0, 0, 0)).reshape(1, 5)
# Chosen st. (Sc + Sg) * x0 = 1
Sb = np.array((0, 0, 0, 0, 2.135)).reshape(1, 5)
Ss = np.array((0, 0, 0, 0, 0)).reshape(1, 5)
economy = Economy(β=β, Sg=Sg, Sd=Sd, Sb=Sb,
Ss=Ss, discrete=False, proc=(A, C))
T = 50
path = compute_paths(T, economy)
gen_fig_1(path)
gen_fig_2(path)

12.3.1. Comments on the Code#
The function
var_quadratic_sumimported fromquadsumsis for computing the value of (12.11) when the exogenous processBelow the definition of the function, you will see definitions of two
namedtupleobjects,EconomyandPath.The first is used to collect all the parameters and primitives of a given LQ economy, while the second collects output of the computations.
In Python, a
namedtupleis a popular data type from thecollectionsmodule of the standard library that replicates the functionality of a tuple, but also allows you to assign a name to each tuple element.These elements can then be references via dotted attribute notation — see for example the use of
pathin the functionsgen_fig_1()andgen_fig_2().The benefits of using
namedtuples:Keeps content organized by meaning.
Helps reduce the number of global variables.
Other than that, our code is long but relatively straightforward.